What is Regression?

Regression is one of the main applications of the supervised Machine Learning.

Its origins are in other field, bit like in statistics, Regression in ML is used to search for association between independent variables and outcomes or dependent variables. Algorithm in continuous iterations can generate outcomes to given features.

These abilities make Regression models valuable in forecasting stock prices, user trends in e-commerce, mortgage rates, health insurance allowance and many more from variety of factors. However, to achieve this feat, models need to be properly trained and input labeled. In training process model teaches itself about relations between given input and output data. Training data should be vast enough to represent overall population and extra care taken in preparing it to not overfit model with unlinked details. Regression technique is used to find time series, correspondence between variables, predictor strenght and/or cause and effect relation.

Properly trained model is huge aid in finding connections in big data and creating prognostics in many different fields like science or business.

Use cases

  • Predictive Modeling:

    • Stock Price Prediction: Predicting future stock prices based on historical price data, trading volumes, and other relevant factors.
    • Sales Forecasting: Forecasting future sales or revenue based on past sales data, marketing expenditures, economic indicators, and seasonal trends.
    • Demand Forecasting: Predicting demand for products or services based on factors such as price, promotions, seasonality, and market conditions.

  • Financial Analysis:

    • Risk Assessment: Assessing credit risk for loans or investments by predicting the likelihood of default based on financial metrics, credit scores, and other factors.
    • Portfolio Optimization: Optimizing investment portfolios by predicting asset returns and volatility based on historical data and market factors.
    • Insurance Premium Estimation: Estimating insurance premiums for policies based on risk factors such as age, health status, and driving history.

  • Marketing and Customer Analytics:

    • Customer Lifetime Value Prediction: Predicting the lifetime value of customers based on past purchase behavior, demographics, and engagement metrics.
    • Churn Prediction: Identifying customers at risk of churn (i.e., discontinuing services) based on usage patterns, satisfaction scores, and customer interactions.
    • Market Segmentation: Segmenting customers into groups based on similarities in purchasing behavior, demographics, and preferences.

I don't really get all that Regression

Do not worry, we got you.

Even thou reality is much more convoluted we can analyze situation of exemplary amusement park and relation between ticket price and how happy guests were.

  1. Gather data

We give quick survey to random guests leaving park to grade on scale how satisfied they are after visit. Let’s say we do it for a 2 years and we don’t build new rollercoasters, only change prices of tickets. That way we have independent variable – ticket price, and dependent – client satisfaction.

  1. Plotting data

We can visualize our data on simple plot. On y-axis we put satisfaction, and prices on the x-axis. Now correlation between those two variables should be easily seen.

  1. Regression line

Regression line is summary of relation between our independent (ticket price) and dependent (customer satisfaction) variables. It can be calculated easily with Excel or other spreadsheet program, but we prefer approach it with Machine Learning in mind 😊.

  1. Understanding Regression

We can most probably observe that rising prices without offering new, exciting attractions causes drop of ticket sales. Also not everybody has same tastes and guests are going to have different opinions about our park.

That is when Regression line comes in handy, showing us how reviews change depending on ticket price, depending on all gathered data.

Now imagine doing this with much, much more evidence, like time of the season or day, weather, waiting in queues, building new attractions, food quality, etc.

Wouldn’t it be easier to leave it for model to analyze?

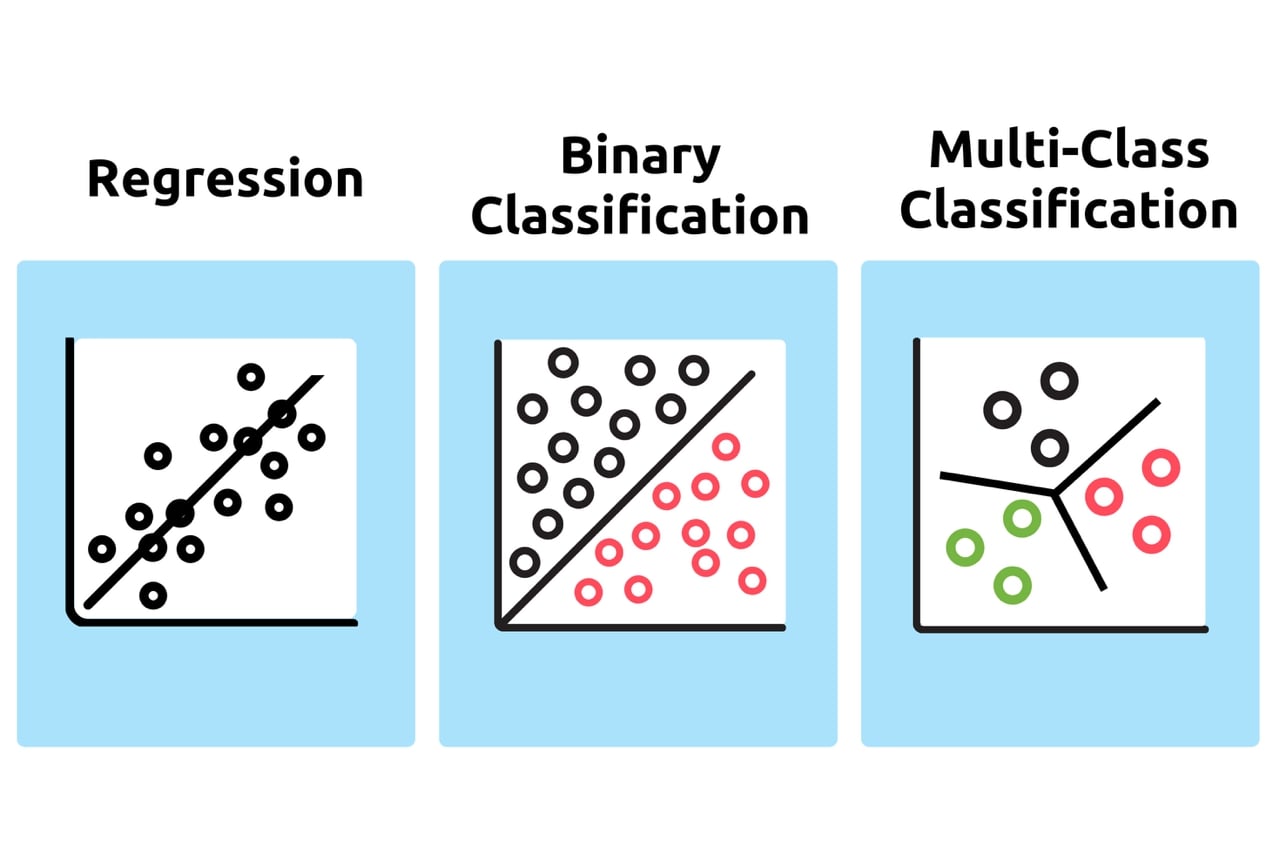
Graphical representation of Regression, binary classification and multi-class classification

Many types of Regression

In Machine Learning we can find plenty of different types of regressions varying accordingly to type of analyzed data.

  • Simple linear Regression

    • The most basic type of Regression in machine learning. Consists of one in- and one -dependent variable. Every value has impact on Regression line.
    • Useful in finding dependencies between variables and forecasting values respectively.

  • Multiple linear Regression

    • Very similar to simple line Regression, used in case of at least two independent variables influencing one dependent variable.
    • Estimation and forecasting within definitive conditions.

  • Logical Regression

    • As you can guess this Regression use binary data set (e.g. Truth or False, 0 or 1). Could be use in mitigating risk of bias occurrence. It is easy to implement too.
    • Its application varies. From binary classification (email spam) through healthcare (predicting disease based on symptoms) to advertisement (advertisement click worth).

  • Lasso Regression

    • Lasso Regression isn’t actually connected to Wild West. It is an abbreviation to Least Absolute Shrinkage and Selection Operator and it’s a linear Regression technique.
    • Thanks to regularization term it prevents overfitting and “motivates” model to minimize amount of coefficients in multivariable datasets.
    • Benefit of this are simpler and easier to read models because of focus that technique on sparse connections between variables. It truly is an amazing tool for those working with multi-dimensional datasets and searching for simplified correlation.

Error menagment

In Regression analysis, error management involves understanding and managing the errors or residuals produced by the Regression model. Errors represent the discrepancy between the actual target values and the predicted values generated by the Regression model. Effective error management is crucial for assessing the model's performance, diagnosing potential issues, and improving predictive accuracy.

  1. Residual Analysis: Residual analysis is a fundamental technique for error management in Regression. It involves examining the residuals (the differences between actual and predicted values) to assess the model's fit to the data. Residual plots, such as scatter plots of residuals against predicted values or independent variables, can reveal patterns, trends, or heteroscedasticity (unequal variance) in the errors.
  2. Diagnostic Measures: Several diagnostic measures can be used to quantify the goodness of fit and identify potential problems with the Regression model. Common diagnostic measures include the coefficient of determination (R-squared), mean squared error (MSE), root mean squared error (RMSE), mean absolute error (MAE), and residual plots.
  3. Outlier Detection: Outliers are data points that deviate significantly from the overall pattern of the data. Outliers can have a disproportionate impact on the Regression model, leading to biased parameter estimates and reduced predictive accuracy. Identifying and managing outliers is essential for improving the robustness of the Regression model.
  4. Model Assumptions: Regression models are based on certain assumptions, such as linearity, independence of errors, homoscedasticity (constant variance), and normality of residuals. Violations of these assumptions can lead to biased estimates and inaccurate predictions. Error management involves assessing whether these assumptions hold and taking appropriate corrective actions if necessary.

Overall, effective error management in Regression analysis requires a thorough understanding of the data, the Regression model, and the underlying assumptions. By systematically analyzing errors and addressing potential issues, practitioners can build more reliable and accurate Regression models for predictive modeling and decision-making.

Linear Regression in Python

You can easily use Regression analysis in Python with the help of various libraries and packages. One of the most popular libraries for Regression analysis in Python is scikit-learn (sklearn). Scikit-learn provides several toy datasets that can be easily loaded and used for experimentation and learning purposes. These datasets are included in the sklearn.datasets module.

Here's an example of how you can load one of the toy datasets, specifically the Boston House Prices dataset, and perform linear Regression on it:

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# Load the Boston House Prices dataset
boston = load_boston()
X = boston.data  # Features
y = boston.target  # Target variable

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Initialize Linear Regression model
model = LinearRegression()

# Train the model on the training data
model.fit(X_train, y_train)

# Make predictions on the test data
predictions = model.predict(X_test)

# Evaluate the model
mse = mean_squared_error(y_test, predictions)
print("Mean Squared Error:", mse)

In this example, we load the Boston House Prices dataset using load_boston() from sklearn.datasets, split it into training and testing sets using train_test_split, initialize a Linear Regression model, train the model on the training data, make predictions on the test data, and evaluate the model using mean squared error.

Pros and cons

Regression seems like an amazing tool and it is. It's qualities to make predictions about continuous outcomes based on historical data and observed patterns can make it a great weapon in your ML arsenal. However there can be some difficulties:

  • Advantages:

    • Interpretability - Linear Regression models are easy to interpret, as they provide coefficients that represent the relationship between the input features and the target variable. These coefficients indicate the magnitude and direction of the effect of each feature on the target variable.
    • Simple and Fast - Linear Regression is computationally efficient and can be trained quickly, especially for large datasets with many features. This makes it suitable for applications where real-time predictions are required.
    • Versatility - Regression analysis can be applied to various types of data and is not limited to specific domains. It can be used in fields such as finance, healthcare, marketing, engineering, and environmental science.

  • Disadvantages:

    • Assumption of Linearity - Linear Regression assumes a linear relationship between the input features and the target variable. If this assumption is violated, the model may produce biased or inaccurate predictions.
    • Overfitting - Linear Regression models can be prone to overfitting if the model is too complex relative to the amount of data available. This can result in poor generalization to new, unseen data.
    • Limited Flexibility - Linear Regression is limited in its ability to capture complex relationships between variables, especially if the relationships are non-linear or involve interactions between features.

Literature

Conclussion

In conclusion, Regression in Machine Learning is a technique used for predicting continuous numerical values based on input features. It involves finding the relationship between independent variables (features) and a dependent variable (target) through training.

Regression models aim to minimize the difference between predicted and actual values, often using algorithms like Linear Regression. Regression is widely applied in various fields including finance, economics, healthcare, and engineering for tasks such as predicting stock prices, estimating house prices, forecasting sales, and analyzing trends in data.