How many trees in the Random Forest?

I have trained 3,600 Random Forest Classifiers (each with 1,000 trees) on 72 data sets (from OpenML-CC18 benchmark) to check how many trees should be used in the Random Forest. What I've found:

• the best performance is obtained by selecting the optimal tree number with single tree precision (I've tried to tune the number of trees with 100 trees and single tree step precision),
• the optimal number of trees in the Random Forest depends on the number of rows in the data set. The more rows in the data, the more trees are needed (the mean of the optimal number of trees is 464),
• when tuning the number of trees in the Random Forest train it with maximum number of trees and then check how does the Random Forest perform with using different subset of trees (with single tree precision) on validation dataset (code example below).

The details of my study is below. The link to all code in Jupyter Notebook. If you have any questions, you can email me at: piotr@mljar.com or leave a comment.

The Data Sets From OpenML-CC18 Benchmark

The data sets used in this study are from OpenML-CC18 benchamrk. Each dataset were carefully selected from thousands of data sets on OpenML by creators of the benchmark.

In the plot below are presented distribution of the number of rows and columns in the datasets, and scatter plot with data sizes:

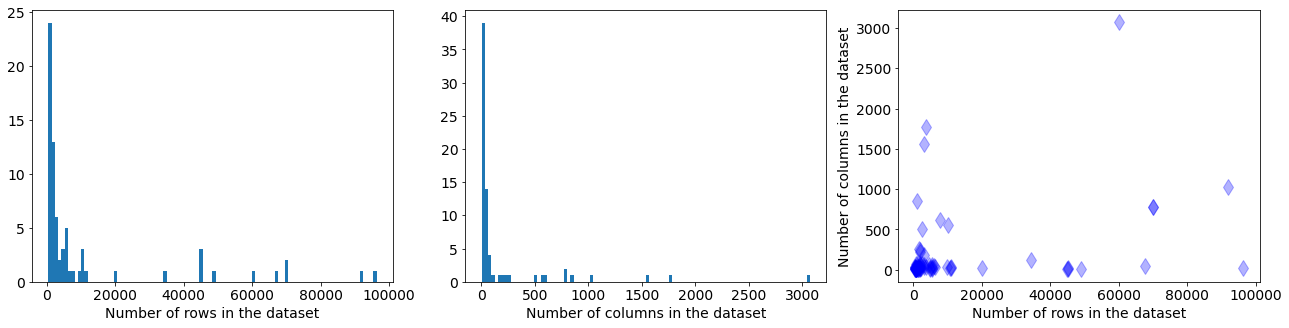
Most of the datasets have up to few thousands rows and up to hundred columns - they are small and medium sized datasets. Eeach data set in the benchmark suite has a defined train and test splits for 10-fold cross-validation.

Training the Random Forest Classifiers with Scikit-Learn

For each train and test split I added 5-fold cross-validation (internally), so I have a validation data which can be used to tune the number of trees. To make it clear:

• each data set has defined train and test split (with 10-fold CV),
• for each train data, I additionally split it into train and validation with 5-fold CV,
• for each set of (train, validation, test) data I have trained a Random Forest classifier from scikit-learn with n_estimators=1000 (other hyper-parameters are left default).

The code to train and save the Random Forests models:

# load packages
import os
import openml
import joblib

import pandas as pd
import numpy as np

from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import log_loss
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import StratifiedKFold

Set constants:

openml.config.apikey = "af03aa0fe70d3aed007035c74222e658" # my old OpenML API
DIR = "where-to-save-rf-models"
TOTAL_TREES = 1000

benchmark_suite = openml.study.get_suite('OpenML-CC18') # obtain the benchmark suite

Train and save the Random Forests. Please note, that while saving the model (with joblib.dump) I set the compress=3 which reduces the model file size (sometimes even up to 5 times).

def train_random_forest(X, y, fname_prefix):
    # train Random Forest with internal 5-fold CV
    skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=1234)
    for fold, (train_index, validation_index) in enumerate(skf.split(X, y)):
        X_train, X_validation = X[train_index], X[validation_index]
        y_train, y_validation = y[train_index], y[validation_index]
        
        model = RandomForestClassifier(n_estimators=TOTAL_TREES, random_state=1234, n_jobs=-1)
        model.fit(X_train, y_train)
        joblib.dump(model, fname_prefix + f"_f_{fold}", compress=3)
        

for task_id in benchmark_suite.tasks:  # iterate over all tasks
    task = openml.tasks.get_task(task_id)  # download the OpenML task
    X, y = task.get_X_and_y()  # get the data
    
    # basic preprocessing
    df = pd.DataFrame(X)
    to_remove = []
    for col in df.columns:
        empty_column = np.sum(pd.isnull(df[col]) == True) == df.shape[0]
        constant_column = len(np.unique(df.loc[~pd.isnull(df[col]), col])) == 1
        if empty_column or constant_column:
            to_remove += [col]
    # remove constant and empty columns
    df.drop(to_remove, inplace=True, axis=1)
    # fill missing values with mode
    df_mode = df.mode().iloc[0]
    df = df.fillna(df_mode)
    X = np.array(df) # back to numpy array
    
    # repeat 10 times (10-fold CV)
    n_repeats, n_folds, n_samples = task.get_split_dimensions()
    for fold in range(n_folds):
        train_indices, test_indices = task.get_train_test_split_indices(repeat=0, fold=fold, sample=0)
        X_train = X[train_indices]
        y_train = y[train_indices]
        X_test = X[test_indices]
        y_test = y[test_indices]

        fname_prefix = os.path.join(DIR, f"task_{task_id}_repeat_{fold}_rf")
        train_random_forest(X_train, y_train, fname_prefix)

Compute the Performance of the Random Forest Classifier

To compute the model's performance I use the test data and logloss metric. I check what is the performance of the Random Forest with [100, 200, 300, 400, 500, 600, 700, 800, 900, 1000] trees. Please notice, that I'm not training 10 Random Forests models with different number of trees! I'm reusing the Random Forest with 1000 trees, with setting different numer of n_estimators before prediction. This saves a lot of computational time when doing a hyper-parameters search. The final response is the average prediction from the 5 Random Forests (trained with internal 5-fold CV).

In the second approach, I search for the number of trees which will minimize the logloss on validation data. In this method, I iterate over all trees in the forest and compute predictions from single trees. The prediction of the Random Forest is the average from all trees in the subset (I'm doing manually what is done internally in predict_proba in the Random Forest). As ealier, the final response is the average over all 5 models (from internal CV). Notice, that each model from internal CV can have (and have) different number of trees.

The code to compute reponses from Random Forest with 100 trees and 1 tree step.

def compute_performance(X, y, X_test, y_test, fname_prefix):
    FOLDS = 5
    results = {}
    # iterate over trees, with 100 trees step
    for t in range(10):
        trees = 100*(t+1)
        response = None 
        for cv_fold in range(FOLDS):
            model = joblib.load(fname_prefix + f"_f_{cv_fold}") # load model
            model.estimators_ = model.estimators_[:trees]
            proba = model.predict_proba(X_test)
            response = proba if response is None else response + proba
        response /= float(FOLDS) # the final prediction is average from internal cross-validation
        ll = log_loss(y_test, response)
        results[trees] = ll
    
    # check the number of trees with minimum loss on validation data set (1 tree step)
    skf = StratifiedKFold(n_splits=FOLDS, shuffle=True, random_state=1234)
    selected_trees = []
    response = None
    for cv_fold, (train_index, validation_index) in enumerate(skf.split(X, y)):
        X_validation = X[validation_index]
        y_validation = y[validation_index]
        
        model = joblib.load(fname_prefix + f"_f_{cv_fold}") # load model
        y_validation_predicted = None
        losses = []
        # iterate over each tree
        for count, estimator in enumerate(model.estimators_):
            proba = estimator.predict_proba(X_validation)
            y_validation_predicted = proba if y_validation_predicted is None else proba + y_validation_predicted
            losses += [log_loss(y_validation, y_validation_predicted / float(count+1.0))]
         
        # set selected number of trees    
        selected_trees += [np.argmin(losses)]
        model.estimators_ = model.estimators_[:selected_trees[-1]]
        proba = model.predict_proba(X_test)
        response = proba if response is None else response + proba
        
    response /= float(FOLDS)
    ll = log_loss(y_test, response)
    results["Selected"] = ll
        
    return results, selected_trees

The code to aggregate all results:

all_results = {}
all_selected_trees = {}
for task_id in benchmark_suite.tasks:  # iterate over all tasks
    task = openml.tasks.get_task(task_id)  # download the OpenML task
    X, y = task.get_X_and_y()  # get the data
    
    # basic preprocessing
    df = pd.DataFrame(X)
    to_remove = []
    for col in df.columns:
        empty_column = np.sum(pd.isnull(df[col]) == True) == df.shape[0]
        constant_column = len(np.unique(df.loc[~pd.isnull(df[col]), col])) == 1
        if empty_column or constant_column:
            to_remove += [col]

    df.drop(to_remove, inplace=True, axis=1)    
    df_mode = df.mode().iloc[0]
    df = df.fillna(df_mode)
    X = np.array(df)
    
    all_results[task_id] = []
    all_selected_trees[task_id] = []
    n_repeats, n_folds, n_samples = task.get_split_dimensions()
    for fold in range(n_folds):
        train_indices, test_indices = task.get_train_test_split_indices(repeat=0, fold=fold, sample=0)

        X_train = X[train_indices]
        y_train = y[train_indices]
        X_test = X[test_indices]
        y_test = y[test_indices]

        fname_prefix = os.path.join(DIR, f"task_{task_id}_repeat_{fold}_rf")
        results, selected_trees = compute_performance(X_train, y_train, X_test, y_test, fname_prefix)
        
        all_results[task_id] += [results]
        all_selected_trees[task_id] += [selected_trees]

Results

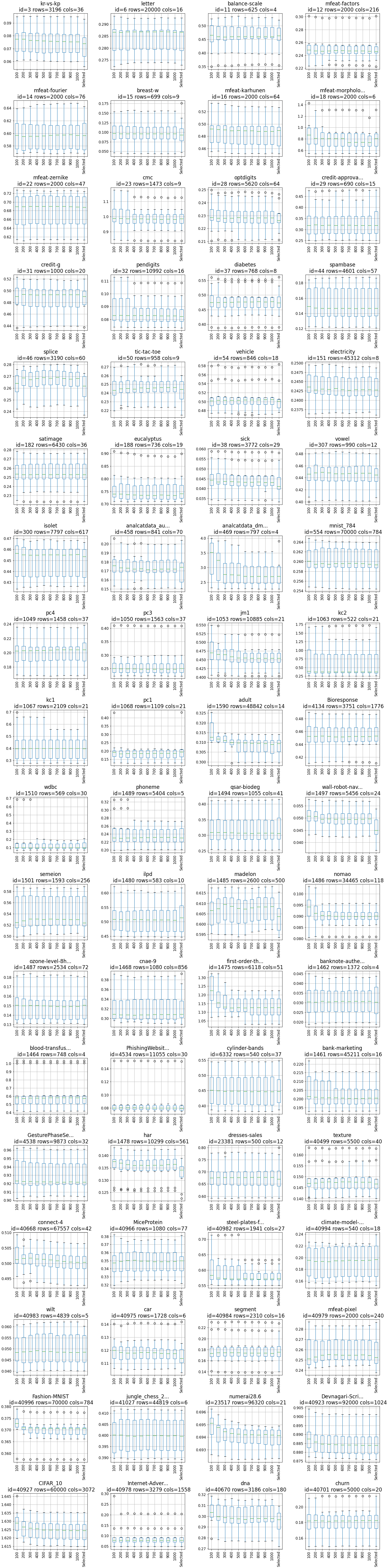
The results are presented as boxplots for each data set. On the x-axis, there is a number of trees. The last box in each plot is the result from optimized number of trees (on x-axis marked as 'Selected'). On the y-axis, there is logloss metric.

To compare all results in the single plot, I used ranking (for each data set and repetition, I ordered the losses and assign rank from 0 to 10 from the best to the worst predictions, so the lowest rank is the best). The average rank is presented below:

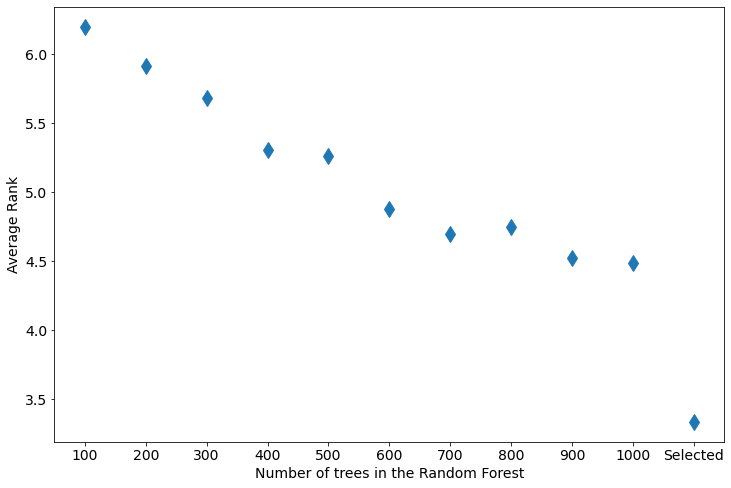
Two things worth to remeber from the above plot:

• the more trees in the Random Forest the performance is better (lower rank),
• however, if the number of trees is tuned with 1 tree step, the performance is significantly better than in the largest forest.

I comupted the mean percentage different between performance of the Random Forest with selected tree number and tree number set with 100 trees step, it is presented below:

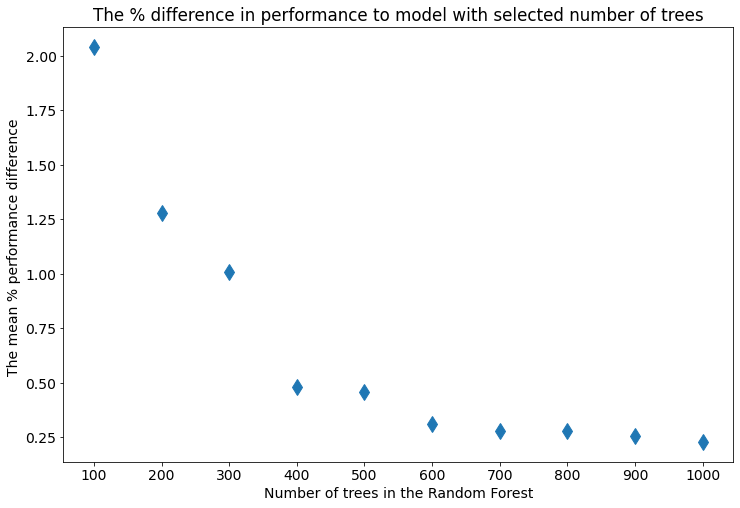
The smallest Random Forest with 100 trees loses about 2% to tuned Random Forest. For ensembles with more than 600 trees, the mean difference is about 0.25%. (Is the 0.25-2% a big improvement? It depends on your task.)

The distribution of the optimized tree number in the Random Forest:

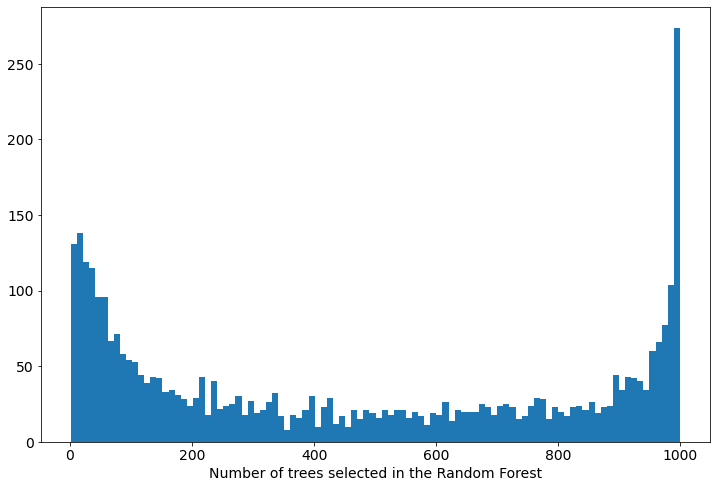
The mean of above distribution is 464, but as you see it is very wide and it will be hard to infer one optmial number of trees in the Random Forest (it strongly depends on the data).

It is interesting, how does the selected number of trees depend on the data set size. There is a strong dependency between number of trees selected in the forest and rows count in the data:

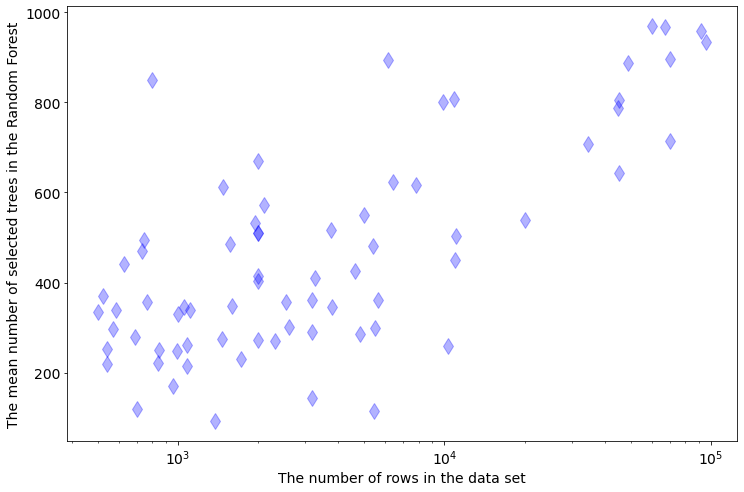
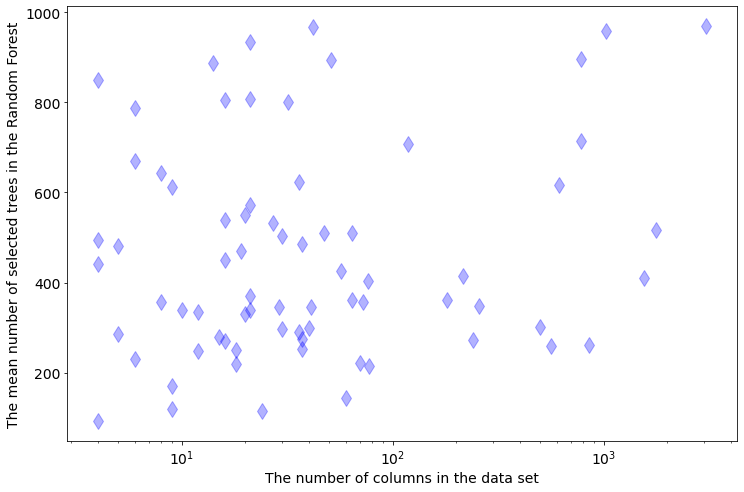
The more rows in the data the more trees are needed. There is not such clear dependency between the selected tree number and number of columns in the data set:

Summary

• It is important to tune the number of trees in the Random Forest.
• To tune number of trees in the Random Forest, train the model with large number of trees (for example 1000 trees) and select from it optimal subset of trees. There is no need to train new Random Forest with different tree numbers each time.
• The number of trees needed in the Random Forest depends on the number of rows in the data set. The more rows in the data, the more trees are needed.
• In MLJAR's open-source AutoML python package mljar-supervised the number of trees is tuned with 1 tree step. The same approach is for Extra Trees algorithm. The details of the implmentation can be found in the Github repository. Maybe it will be nice to have early stopping implementation in the scikit-learn Random Forest.